参考博客：

 

 

结论：

若p是质数，令n=a*p+b，m=c*p+d，  b，d ∈[0,p)

则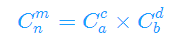

 

 

证明：

 

首先证明 在模p意义下

  

 

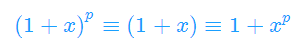
证明法一：

由费马小定理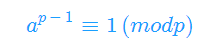， 得

 

 

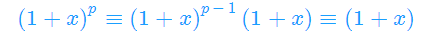
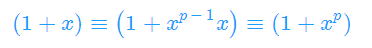
证明法二：

当j∈[1,p-1] 时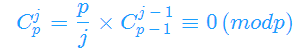， （p是质数，j∈[1,p-1]，j在模p意义下一定有逆元）

用二项式定理展开（1+x）^p

 

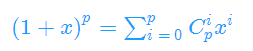
除了第一项和最后一项，中间项的组合数在模p意义下是0

所以

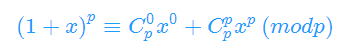
 这张图是盗来的

 

 

 

#include
     
      using namespace std;typedef long long LL;LL f[100001];void pre(int p){    f[0]=1;    for(int i=1;i<=p;i++) f[i]=f[i-1]*i%p;}int pow(LL a,int b,int p){    LL r=1;    while(b)    {        if(b&1) r*=a,r%=p;        b>>=1; a*=a; a%=p;     }    return r;}int C(int n,int m,int p){    if(m>n) return 0; //如果m>n，那么原来的m